Дії над звичайними дробами

 При додаванні (відніманні) дробів з однаковими знаменниками до чисельника першого дробу додають чисельник другого дробу (від чисельника першого дробу віднімають чисельник другого дробу) і залишають той же знаменник. Отриманий дріб, якщо це можливо, скорочують. Наприклад, , .

При додаванні (відніманні) дробів з різними знаменниками переважніше попередньо звести їх до найменшого спільного знаменника. Наприклад, .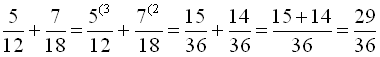

При додаванні мішаних дробів потрібно додати окремо цілі частини і дробові частини. Наприклад,

.

При відніманні мішаних дробів варто розрізняти такі випадки:

a) дробова частина зменшуваного більше або дорівнює дробовій частині від’ємника; у цьому випадку від цілої частини зменшуваного віднімають цілу частину від’ємника, а від дробової частини зменшуваного – дробову частину від’ємника. Наприклад, 

b) дробова частина зменшуваного менше дробової частини від’ємника; в цьому випадку одну з одиниць цілої частини зменшуваного потрібно замінити таким дробом, який їй дорівнює. Наприклад,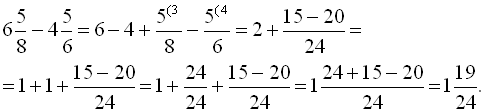 

Множення звичайних дробів виконується таким чином: , тобто перемножують окремо чисельники, окремо знаменники. Перший добуток роблять чисельником, другий – знаменником. Отриманий дріб, якщо це можливо, скорочують.

При множенні мішаних дробів їх попередньо зображають у вигляді неправильних дробів, а потім перемножують. Наприклад, .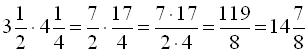

При діленні дробу на дріб чисельник діленого множать на знаменник дільника, а знаменник діленого – на чисельник дільника. Перший добуток служить чисельником, а другий – знаменником частки: 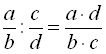. Наприклад, .

Якщо потрібно поділити дріб на дріб, у випадку коли один чи обидва дроби – мішані, то потрібно попередньо зобразити мішаний дріб у вигляді неправильного дробу.

Будь-яку ціле число можна зобразити у вигляді дробу. Наприклад,  , 

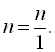
Два числа називаються взаємно оберненими, якщо їх добуток дорівнює 1. Наприклад, 5 і , х і .